Learn how to solve difficult problems from natural evolution process
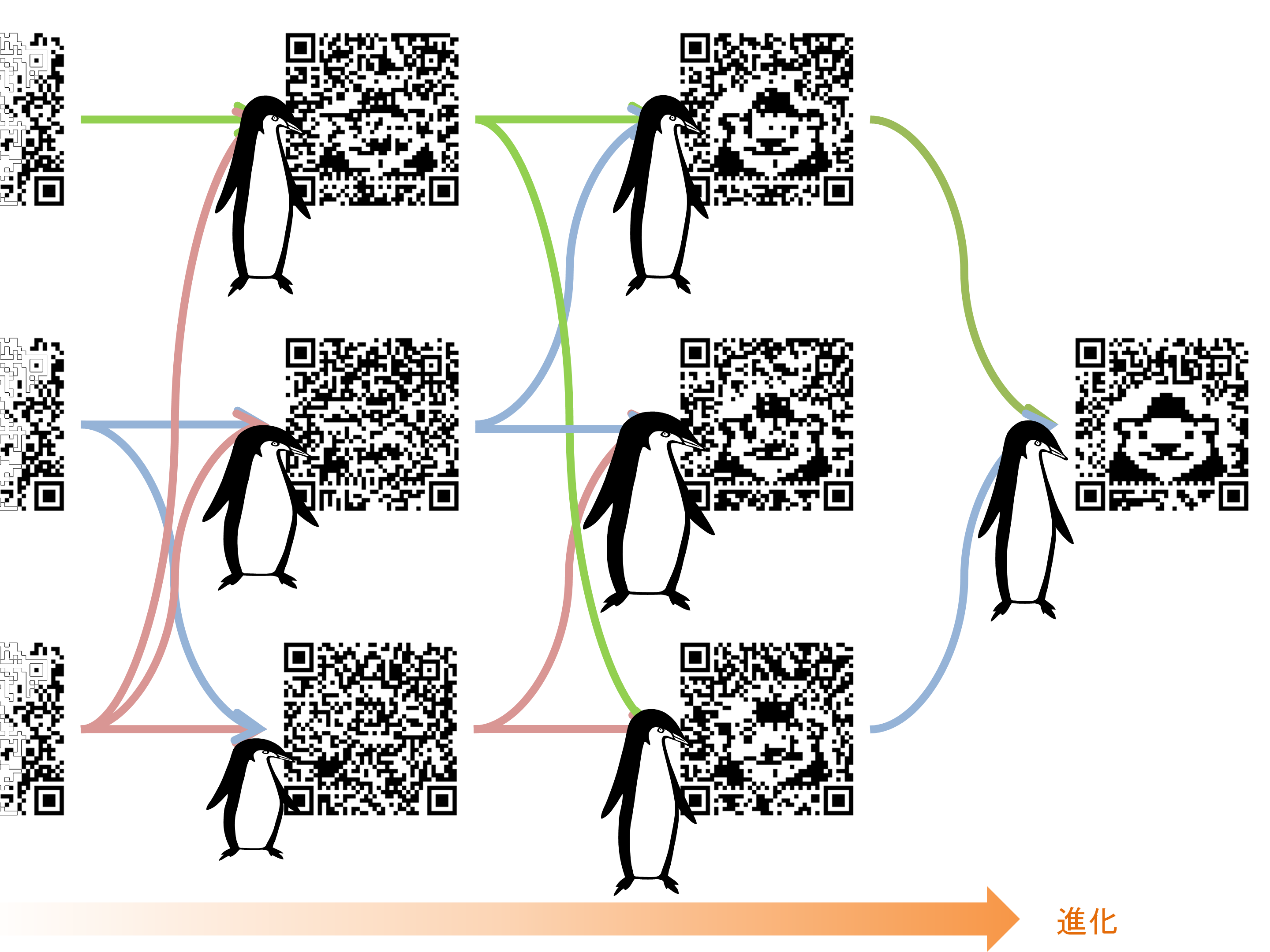
Evolution is a process where organisms acquire their traits adapted to the environment by leaving descendants over the years. Evolutionary computation is a problem solving algorithm that imitates the natural evolution process (*1). Normally, a problem is solved by initially designing and gradually improving just one solution candidate to find a good solution. On the other hand, evolutionary computation algorithms generate a number of solution candidates, such as 100 or 1,000, and regard the candidates as virtual creatures. And these creatures create offsprings. When parents having good traits make offsprings, the offsprings may inherit the good traits of the parents and be a better solution candidate. It is expected that an accumulation of such accidental improvements may effectively solve difficult problems. The right figure shows an example process of evolutionary computation that generates decorated QR codes obeying its standards. When you overlay a picture on a QR code, the picture destroys part of the code and makes it difficult to read when it gets stained. On the other hand, the decorative QR code generated by evolutionary computation can create a module pattern that is visually meaningful to humans without sacrificing any of the QR code functions.
Evolutionary computation algorithms are applicable to various real-world problems
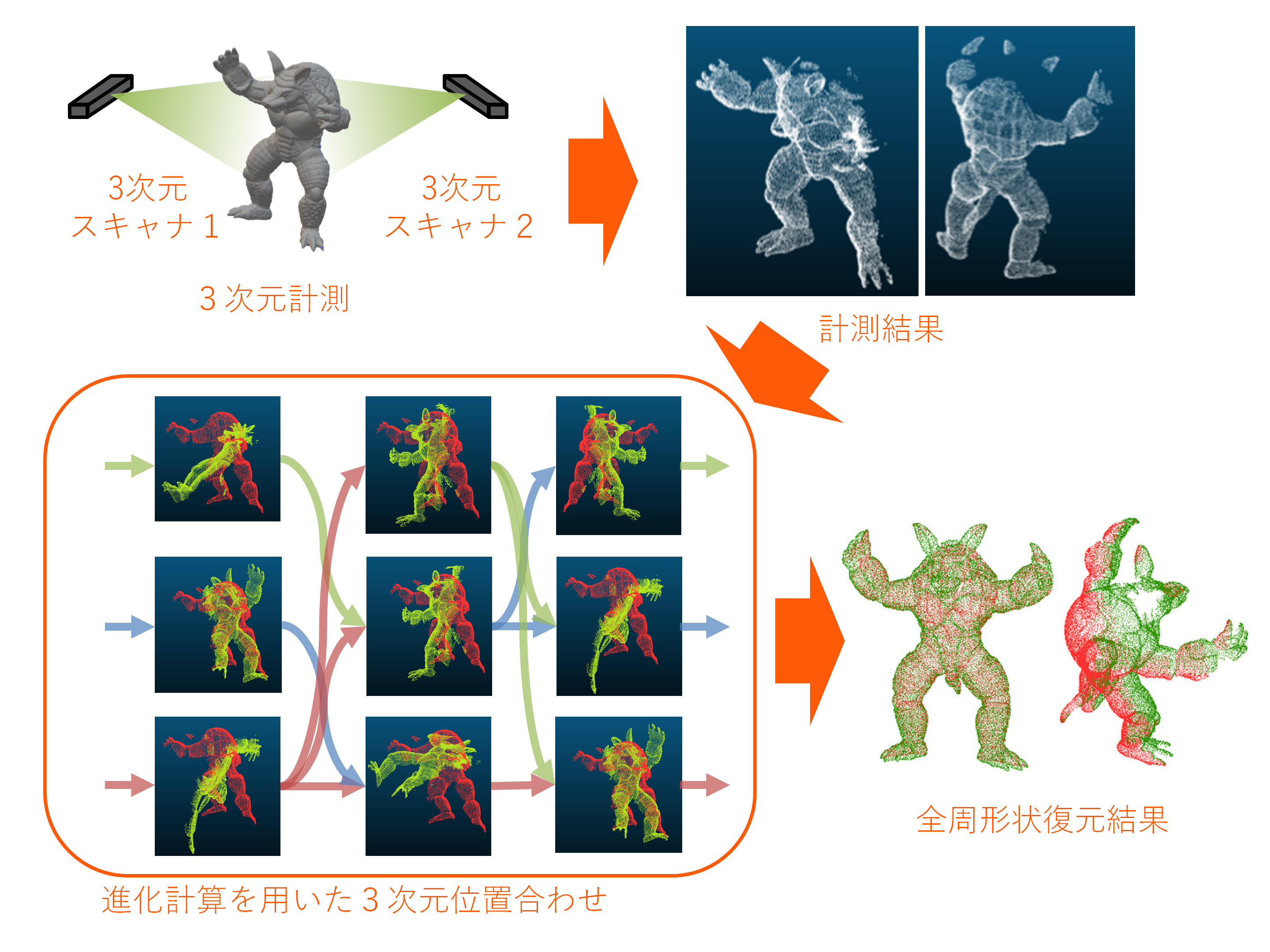
Evolutionary computation is good at solving problems called optimization, and can be applied to various fields such as design, manufacturing, distribution, and finance. Here, we introduce one of our applications to three dimensional (3D) measurements. Generally, when measuring an object using a 3D scanner, it is necessary to measure several times while changing the viewpoint and synthesize the measured partial shapes. The process of aligning the measured 3D shapes is called 3D registration. When using general registration methods, it is necessary to measure four to ten times in order to reconstruct the whole object shape. We developed a new 3D registration algorithm using evolutionary computation. It can find the optimal solution by avoiding falling into local optima (*2), by exploiting the characteristics of evolutionary computation; that is, the property that many solution candidates have simultaneously improved. By incorporating a new objective function (*3) presuming the use of evolutionary computation, the proposed method can reconstruct the entire object shape from the measurement results an extremely small number of times (two or three times, which are the world’s least number of times, to the best of our knowledge).
*1 In particular, evolutionary computation is good at solving optimization problems in which parameters are simultaneously decided so that an objective function should be minimized (or maximized).
*2 Local optima are solutions that have any neighbor better than them.
*3 An objective function is a function that determines how good a solution candidate is.


